Multiplication Hexagons
|
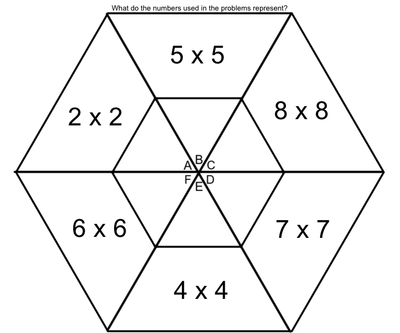
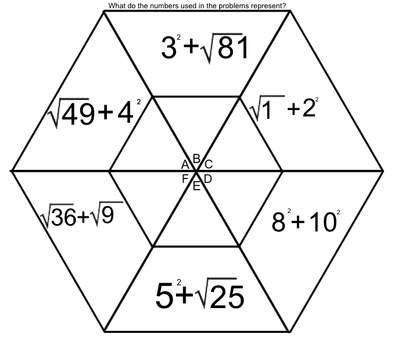
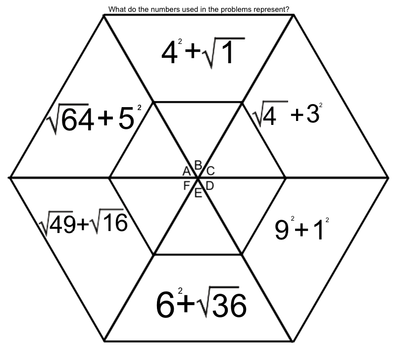
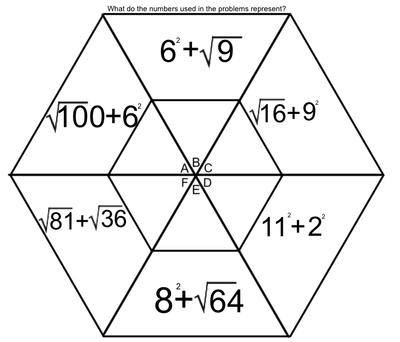
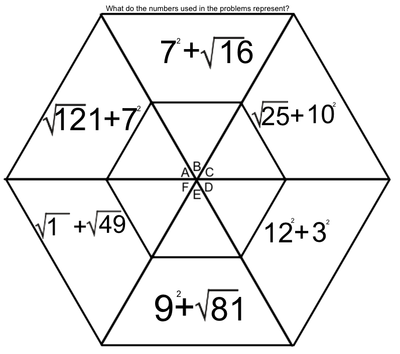
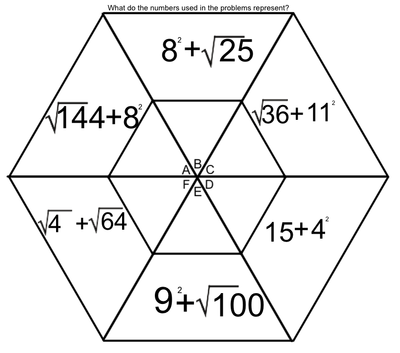
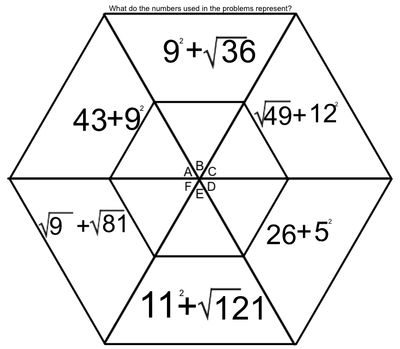
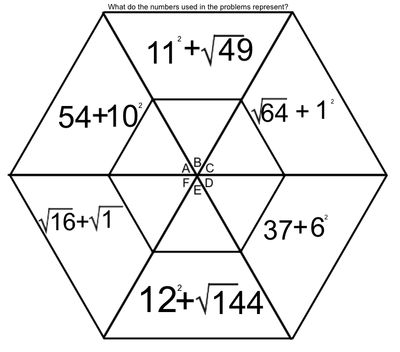
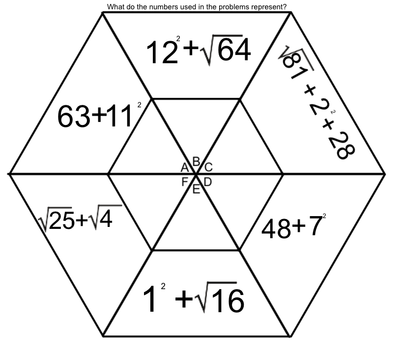
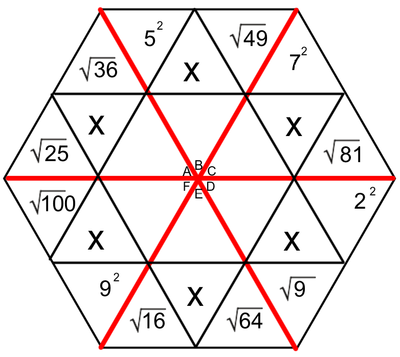
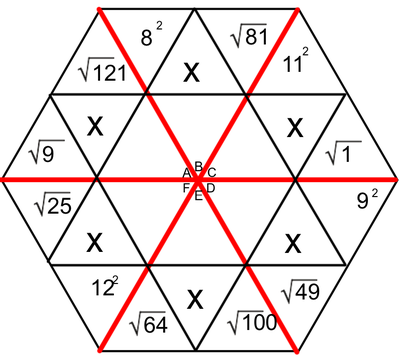
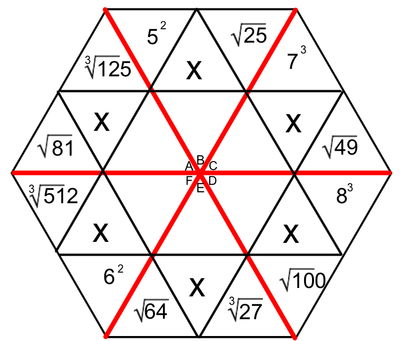
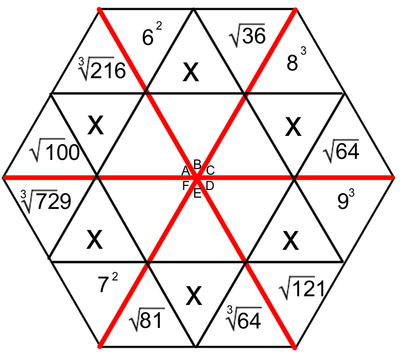
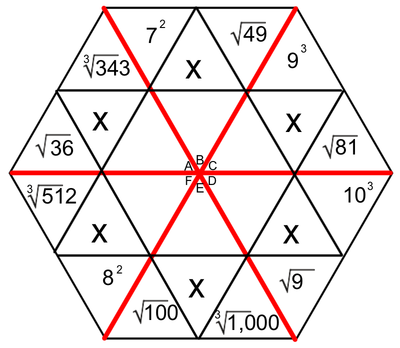
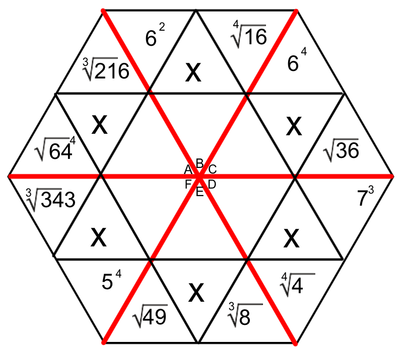
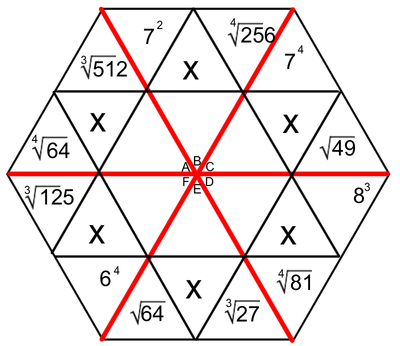
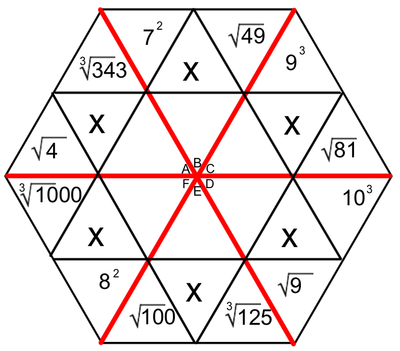
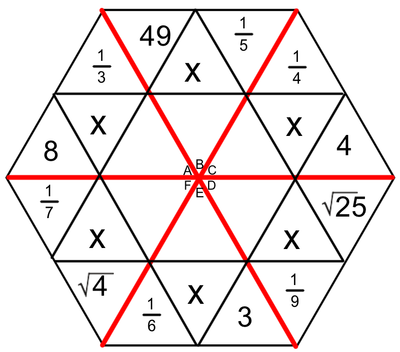
One of the tools we use to enhance multiplication skills are our hexagons. I created the hexagons with the idea that we could work on the basics of multiplication facts, while at the same time learning two-digit (and higher) multiplication (We've made it as far as the figure on the left. Presented here, it's obvious that the hexagons become progressively more involved as the weeks pass. Parents, if you want an explanation of how we answer these in class, please ask your child. Most can do this without much leadership; others still need to work on their basic facts.
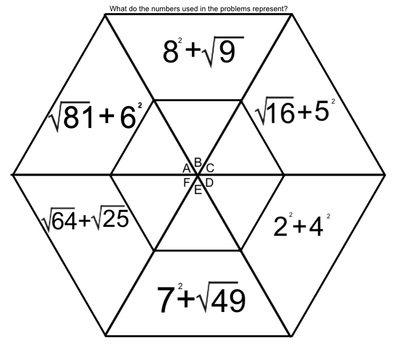
Students love to do these hexagons. During this time, students are successful, not only when they correctly solve a problem, but when they identify the mistakes that caused them to get a problem wrong. Done in a safe way, this identification of mistakes allows students to support and receive support from their peers. They help solve the issues, applaud success, and encourage each other - all as a part of a multifaceted process we have embedded into our class. The hexagons at the end of our official multiplication instruction require higher exponential computation (Doesn't that sound fancy?). We may not get to the most difficult of these, which include cube roots and quad roots. To solve these, students must make some educated guesses (which forces them to work problems with several digits). |
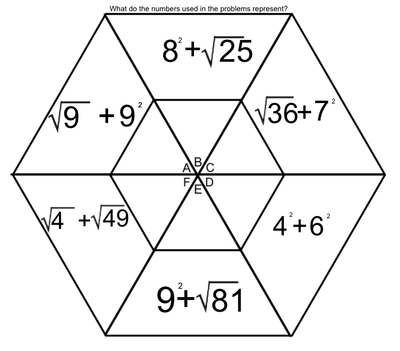
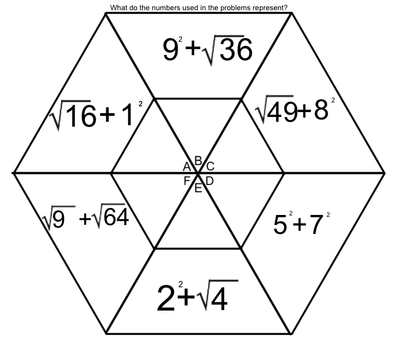
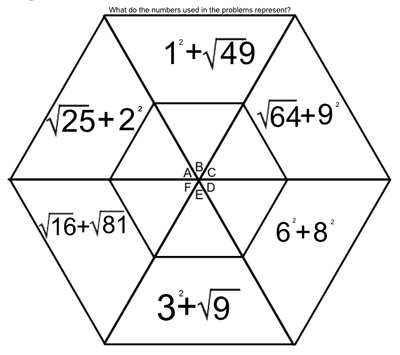
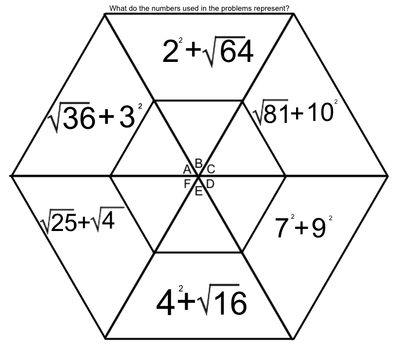
EXPONENTS AND ROOTS REVIEW
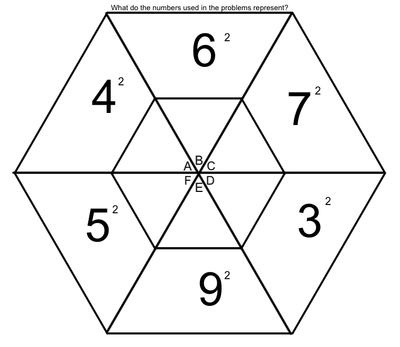
An exponent is that little flying number behind a regular-sized number.
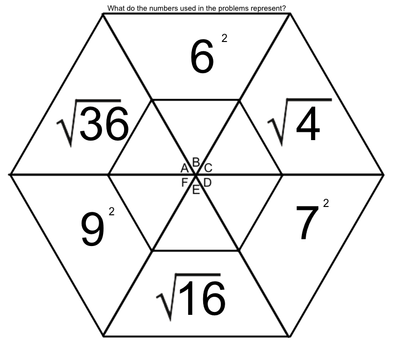
A four with a number two flying behind it is read as "four squared" or "four to the second power". When we see this, we think, 4 x 4. When we see a four with a three flying behind it, we think, 4 x 4 x 4. A square root is very much the opposite of a square number. When we spot the square root of 36, we think, "what number times itself equals 36". |